Problema: in che relazione stanno le grandezze (F e s) che, come sappiamo, definiscono il lavoro meccanico.

Prime osservazioni: notiamo che se lasciamo costante il lavoro e aumentiamo lo spostamento, la forza diminuisce e viceversa.

Ipotesi di soluzione: poiché in matematica, quando una grandezza che noi chiamiamo X (variabile indipendente) assume valori diversi e aumenta e un'altra grandezza ad essa legata che noi chiamiamo Y (variabile dipendente) diminuisce, le due grandezze sono legate da una relazione che potrebbe essere: X + Y = K o X . Y = K, allora possiamo ipotizzare che, nel nostro caso, F . S = K dove K è il Lavoro Meccanico.

Materiale

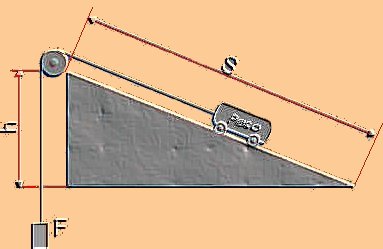
Predisponiamo l'apparecchiatura come nell'illustrazione grafica; per studiare la relazione fra le due grandezze, in base alle ipotesi proposte, variamo "s" e determiniamo F mantenendo costante l’altezza "h" cui il corpo (di Peso costante) viene sollevato dopo lo spostamento "s". Calcoliamo il prodotto fra s e F.

Osservazioni quantitative (tabella e grafico)

I dati in tabella (misurati e calcolati), trascurando gli errori sperimentali, presentano un andamento costante relativamente al prodotto fra s e F; la relazione è rappresentata graficamente nel piano cartesiano da un insieme di punti che si collocano tendenzialmente lungo una linea curva che è un ramo d’iperbole.

 Conclusioni

I dati sperimentali confermano l’ipotesi iniziale che poneva le due grandezze F e s in un rapporto di proporzionalità inversa, cioè in una costanza del loro prodotto, rappresentata dalla funzione matematica X . Y = K