PROBLEMA

Studiare il fenomeno delle mescolanze di sostanze a diversa temperatura.

MATERIALI

Termometro, bicchiere di carta  inserito in un tubo di  gomma espansa, piastra elettrica, acqua: 100 g (M1) a temperatura T1 e 200 g (M2) a temperatura T2; beaker.

PROCEDIMENTO

Preparare una massa d'acqua nota a temperatura ambiente e rilevare la sua temperatura dopo averla versata nel recipiente" isolante", subito prima dell'inizio dell'esperimento; scaldare una massa d'acqua nota con la piastra elettrica e portarla circa a 80°C , e versarla rapidamente, avendo determinato subito prima la sua temperatura , nel contenitore "isolante" che viene subito richiuso. Determinare immediatamente la temperatura della mescolanza così ottenuta.

PREVISIONI

Per prevedere la temperatura finale sono stati effettuati calcoli sui seguenti dati sperimentali:

M1 =100 g

M2 =200 g

T1 = 70,0 °C

T2 = 22,0 °C

Tf = 37,5 °C

 

 

Alcuni studenti: dividiamo per 3 e non per 2, perché la massa totale è 300 g e si può considerare suddivisa in 3 parti uguali di cui una è rappresentata da 100 g e l'altra da 200 g.

Prof.ssa: ma la massa a 22°C è doppia di quella a 70°C !

Studente: allora "vale "il doppio! Quindi devo moltiplicare per 2 il 22!

 

allora... passiamo alla prova sperimentale: la temperatura raggiunta è 37,5 °C (per gli errori sperimentali) quindi la previsione è esatta!

 

Studente: ripetiamo la prova variando la temperatura e la massa.

Riportiamo qui di seguito i dati ottenuti e le nostre previsioni col  metodo ipotizzato così riassumibile:

se una massa è doppia dell'altra la formula è: (massa1  x  1 + massa2  x  2) /  3; se una massa è tripla dell'altra la formula è: (massa1 X 1 + massa2 X 3) / 4; ....

E, in generale, nel caso di una massa non multipla dell'altra: (massa1 x temperatura1 + massa2 x temperatura2)/ somma delle masse.

OSSERVAZIONI QUANTITATIVE

 

 

CONCLUSIONI 

Si può scrivere allora: ( temperatura1 x massa 1+ temperatura2 x massa2) / somma delle masse

 

DIALOGO DIDATTICO

Prof.ssa: come si può rappresentare questo tipo di problema?

Studente: con dei segmenti, le cui lunghezze vengono sommate.

Facciamo delle prove coi segmenti, ma non ci rappresentano la formula ottenuta.

Allora proviamo  a discutere.

Prof.ssa: la massa x la temperatura non si può rappresentare con i segmenti: si tratta di un prodotto!

Studente: è come un'area;  forse va bene il rettangolo!

Riportiamo qui di seguito i modellini ricavati con i rettangoli dopo alcune prove e la formula ottenuta:

 

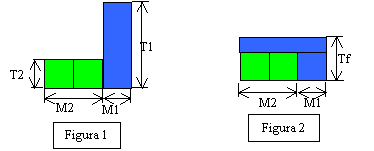
Le figure 1 e 2 sono equiestese: la parte verde rappresenta il prodotto M2.T2 e la parte blu rappresenta il prodotto M1.T1 nella figura 1. Nella figura 2 la parte verde rimane invariata, la parte blu si distribuisce in misura uguale sulle masse. La temperatura finale si  può quindi rappresentare come l'altezza della figura 2 equiestesa alla figura 1 avente la stessa base.

In conclusione:

 

Nota dell'insegnante

La discussione per arrivare ai modellini grafici e alla formula generale ha richiesto abbastanza tempo; è stato necessario richiamare i ricordi di modellini grafici utilizzati per problemi geometrici e aritmetici di " somma di frazioni”.

---

torna al piano di lavoro